十二平均律解释

世界上最早根据数学来制订十二平均律的是我国明朝大音乐家朱载（土育）（1854年）。

    半音是十二平均律组织中最小的音高距离。两音间的距离等于两个半音的叫做全音。八度内包括有十二个半音，也就是六个全音。

    在音列的基本音级中间，除了E到F、B到C是半音外，其余相邻两音间的距离都是全音。

    在钢琴上，相邻的两个琴键（包括黑键）都构成半音，隔开一个琴键的两个音则都构成全音。

首先我们要说一下音乐的基本科学属性。音乐，主要是由声波来传递的，从物理上来讲，声波由各种各样的物理量来描述。这些物理量中用来区别不同的音的，是频率。所以我们说一个音是“高音”，或者“低音”，这个高和低指的就是音的频率的高低。
在定义了音和音的区别之后，我们就可以定义什么叫做一个八度了。如果我们说这两个音之间差八度，指的就是这两个音之间的频率之比为2。如果你脑子比较快，可能看到这个八度的定义就能猜出12平均律啥意思了，所谓把八度平均分城12等分，意思就是一个8度13个音，相邻两个音之间的频率之比相等（注意啊，是频率之比，不是频率之差）。这个比为2的12次方根：2^(1/12)=1.059463........

进而有人定义了一个基准音的频率——高音A:440Hz，于是所有音的频率就此全部定下来了。列出整个高音八度为例(频率近似表示为整数)：
C(高音C)   :262Hz 
#C(bD)     :277Hz
D             :294Hz
#D(bE)     :311Hz
E              :330Hz
F              :349Hz
#F(bG)     :370Hz
G             :392Hz
#G(bA)     :415Hz
A             :440Hz
#A(bB)     :466Hz 
B             :494Hz
C(倍高音C):523Hz

如果你是一个合格的科技工作者，估计有几个疑问马上就会跳出来：
1.为什么是这么个平均法：
     为什么是频率之比相等而不是频率之差相等？
     那是因为8度是通过频率之比定义的，否则岂不是不同八度里的频率公差是不一样的？如果你一定要追根究底为什么8度是通过频率之比定义的……我后面会提到的

2.为什么是“十二”平均律，而不是什么十平均律：
     这也是我当初最不能理解的地方。无论是“2的12次方根”或者1.059463.....都不是什么漂亮的数字或者表达，为什么如此美妙的音乐，其基础理论会出现这么恐怖的数字呢。巴赫也就算了，那个时候西方已经有了无理数这个概念，就算他哪天脑子被一本名为《2的12次方根》的书砸了一下就蹦出来这个基础乐理也就算了。但是朱载堉呢？而且如果你还记得初中音乐课的内容，中国古代的五声体系“宫商角徵羽”对应的是12平均律里的CDEGA。几千年前的人们怎么能殊途同归地整出这么变态的数字呢？

解答Part I：
之前说了音和音的区别就是频率的区别。但是音乐的主要目的是和谐的，而并不是随便的一个频率组合都是和谐的。那怎么样的频率组合是和谐的呢？这个问题可能要取决于不同的人的听觉了。但是似乎从人类历史上的经验来，似乎越简单的频率组合听上去越舒服。这样我们就可以入手了。
首先是1:1   哦，对，这就是同一个音……
然后是1:2   这是什么？这就是八度音程，所以我们定义八度不是瞎定义的，这是最简单的频率组合
一般我们习惯于只考虑一个八度之内(频率之比小于2)的音程
所以接下来就是2：3了
然后是3：4，3：5
然后是4：5， 4：7
..........................
那十二平均律里的的频率之比和这些最和谐的频率之比又是什么关系呢?
(热泪盈眶的找到了这张图……)

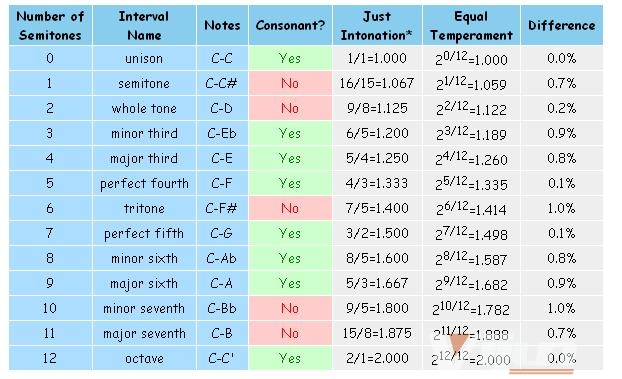
不难发现，所有我之前所说的几乎所有的和谐的频率组合在12平均律里都有非常近似的表示。且期中最主要的两个3/2和4/3的近似也是非常好，所以这两个音程叫perfect fourth和perfect fifth。
有兴趣用别的平均律的可以试试，能不能凑出这么接近的结果且没有太多不和谐音程的，好像是找不出更好的了吧。

于是我们再回过头来看中国的“宫商角徵羽”对应于CDEGA，中国古代的音乐其实是基于9/8,5/4,3/2和5/3这几个频率之比而不是十二平均律中那些个变态的无限不循环小数的频率之比的。中国古人虽然数学理论差了点，但是这些个基本的比例还是很早就掌握了的。